Musselman's theorem
In Euclidean geometry, Musselman's theorem is a property of certain circles defined by an arbitrary triangle.
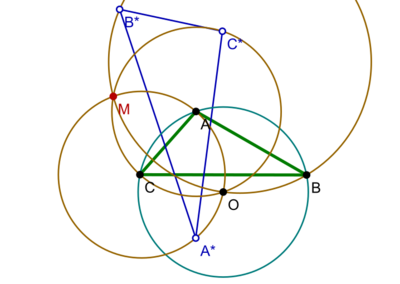
Specifically, let be a triangle, and , , and its vertices. Let , , and be the vertices of the reflection triangle , obtained by mirroring each vertex of across the opposite side.[1] Let be the circumcenter of . Consider the three circles , , and defined by the points , , and , respectively. The theorem says that these three Musselman circles meet in a point , that is the inverse with respect to the circumcenter of of the isogonal conjugate or the nine-point center of .[2]
The common point is point in Clark Kimberling's list of triangle centers.[2][3]
History
The theorem was proposed as an advanced problem by John Rogers Musselman and René Goormaghtigh in 1939,[4] and a proof was presented by them in 1941.[5] A generalization of this result was stated and proved by Goormaghtigh.[6]
Goormaghtigh’s generalization
The generalization of Musselman's theorem by Goormaghtigh does not mention the circles explicitly.
As before, let , , and be the vertices of a triangle , and its circumcenter. Let be the orthocenter of , that is, the intersection of its three altitude lines. Let , , and be three points on the segments , , and , such that . Consider the three lines , , and , perpendicular to , , and though the points , , and , respectively. Let , , and be the intersections of these perpendicular with the lines , , and , respectively.
It had been observed by Joseph Neuberg, in 1884, that the three points , , and lie on a common line .[7] Let be the projection of the circumcenter on the line , and the point on such that . Goormaghtigh proved that is the inverse with respect to the circumcircle of of the isogonal conjugate of the point on the Euler line , such that .[8][9]
References
- ↑ D. Grinberg (2003) On the Kosnita Point and the Reflection Triangle. Forum Geometricorum, volume 3, pages 105–111
- ↑ 2.0 2.1 Eric W. Weisstein (), Musselman's theorem. online document, accessed on 2014-10-05.
- ↑ Clark Kimberling (2014), Encyclopedia of Triangle Centers, section X(1157) . Accessed on 2014-10-08
- ↑ John Rogers Musselman and René Goormaghtigh (1939), Advanced Problem 3928. American Mathematical Monthly, volume 46, page 601
- ↑ John Rogers Musselman and René Goormaghtigh (1941), Solution to Advanced Problem 3928. American Mathematics Monthly, volume 48, pages 281–283
- ↑ Jean-Louis Ayme, le point de Kosnitza, page 10. Online document, accessed on 2014-10-05.
- ↑ Joseph Neuberg (1884), Mémoir sur le Tetraèdre. According to Nguyen, Neuberg also states Goormaghtigh's theorem, but incorrectly.
- ↑ Khoa Lu Nguyen (2005), A synthetic proof of Goormaghtigh's generalization of Musselman's theorem. Forum Geometricorum, volume 5, pages 17–20
- ↑ Ion Pătrașcu and Cătălin Barbu (2012), Two new proofs of Goormaghtigh theorem. International Journal of Geometry, volume 1, pages=10–19, ISSN 2247-9880
